

左のキャラはIOCといって弊社教材、特に数学で、大切な考え方を伝えるときに出てくるキャラです。
彼の口ぐせである「結論からおむかえ」
IOCの中でももっとも重要な考え方です。
今回はこれについてお話しします。
「図形の問題には発想力が必要」なんて嘘です。
数年後に控えた大学入試制度改革に伴い、「新傾向」「新学力観」と呼ばれる問題が学調テストや入試でますます増加傾向にあります。
そういう問題に対処できるようになるためにも、大切な考え方です。
(スマホでもご覧いただけますが、図形をみながら説明を読んだ方がいいので、できればパソコンの画面でご覧ください。)
先日(2017年1月12日)に行われた、中学第2学年学力調査テスト数学からの引用です。
これ自体はそれほど難しい問題ではありません。
簡単なところで説明した方がわかりやすいでしょうから、この問題を使って説明させていただきます。
図1

図1)28年度 静岡県学力調査テスト中学2学年から引用。
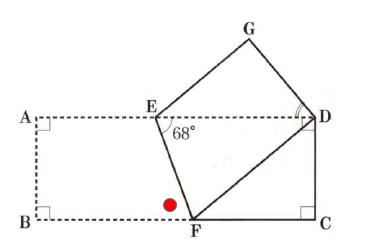
図は、長方形を折り曲げた図。
問題は「∠GDE(図の●)の大きさを求めよ」というものでした。
正式に配布される模範解答では、次のように始まります。
AD//BCより、平行線の錯角は等しいので
∠EFB=∠FED=68°
(図2の●で示した所が、 68°と書かれている部分と同じ大きさだということです。)
図2
言っていることは正しいのですが、おやっ?って思いませんか。
求めよ、といわれている角からなぜそんなに離れたところから考え始めなくてはいけないのでしょうか?(こういう考え方って、実はものすごく正しいです。)
富士宮教材開発の教材では、ここから考え始めるように導きます。
近いところから考えればよいです。
図3

求めたい角度、∠GDEは、∠GDFに含まれる角度です。
長方形を折り曲げた形なので、∠GDF=90°です。(図3赤線で直角を示したところです)
図4

なので∠GDEの大きさを求めるためには・・・
∠EDF(図の●)の大きささえわかれば、90°からその大きさをひいて答えです。
これで「目標」が∠EDFの大きさだと決まります。(こういう答えの肝(きも)となることを、「目標」という言い方をします。)
∠EDFの大きさを求めます。
何を使えばいいでしょうか?
これも近いところから探しましょう。
求めたい∠EDFと、具体的に68°が含まれている三角形があります。
△EDFの内角の和(180°)(図5、赤線で囲んだ三角形)を使えば求められます。
ということで、次の目標は∠EFD(図5の●)です。
図5

図6

もともと長方形を折り曲げてできた形なので、∠EFDの大きさは、∠EFBの大きさと同じです。
ですから、∠EFBの大きささえわかれば大丈夫です。
図7

∠EFBの大きさを求めるために、模範解答では一番最初に出てきた平行線の錯角を利用します。(ここまで何も特別なことはしていません。近いところから考えていっただけです。)
あとは大丈夫ですよね。
180°ー(68°+68°)から∠EDFの大きさを出して、それを90°からひいて答えです。
〔求め方〕の欄には、模範解答と同じようなことを書くことになりますが、解答を書き始める時点で答えまでの道のりがみえています。
やみくもに平行線の錯角から始めるのと、大きな違いがありますよね。
(もっとも、平行線が与えられたから錯角を使うのだろうというのも大切な視点ですが、それはまた別の話です。)
解答だけ見ながら勉強してもあまり学習効果がない、っていうのはこういうことです。
どうやら世間には模範解答をみながら、そのまま書いてあることを説明するだけの先生も多いようです。
そういう先生からすると、「図形問題には発想力が必要」「わかるところからどんどん調べていけばいい。難しく考えるから悪いんだ。」ということにもなるのでしょう。
確かに今回程度の問題でしたら、わかるところから調べていけば答えにたどりつけるでしょう。
しかし、近年増加傾向にある「新傾向」「新学力観」と呼ばれる問題には、とてもたちうちできません。(もっともこういう先生たち自身も、たちうちできないでしょうが…)
むしろ今回のような少し簡単めの問題でこういう大切な考え方を育んでいくことが大切だと、富士宮教材開発は考えています。
(※今回はわかりやすいように数学で説明しましたが、英語・国語・理科・社会といった他の4教科も同じです。
入試問題などで、ますます深い理解が求められるようになっています。
本来学問とはそういうものですが、あまりに教育の現場で表面的な指導しかされなくなってしまってきている。
それに歯止めをかける役割を担うのが「新傾向」「新学力観」と呼ばれる問題です。)
「他のところも、こういう教え方してくれればいいのに、」って思いませんでしたか?
なかなか難しいでしょうね。
個々の指導者の能力の問題もありますが、現実的な時間などを含めたコストの問題もあります。
例えば今回扱った問題でも、解答だけなら5行くらいで済みますがこれだけかかってしまいました。
弊社の教材で、公立高校入試の過去問を扱ったものなどは1年分1教科で、なんと最低35ページの分量です。
まあ、こういうものでなければ実際には役に立たないので世に出しても意味がないと考えているのでいいのですが。
以上です。
ご意見・ご感想お待ちしています。
富士宮教材開発
代表 井出真歩
「新傾向」「新学力観」に関する分析・対処法も充実した、今年度(平成29年)静岡県公立高校入試対策用の「過去問解説マニュアル」もあります。
よろしければ参考にしてください。
→右のボタンをクリックしてください。
シェア歓迎します。リンクもフリーです。
