教科書にのっている、多くの人が余弦定理だと思っているあの公式は、実は第2余弦定理です。
では、第1余弦定理とは何か？
左のくまさんたちが持っているものに大きくかかわりがあります。
最近、各高校でこの第1余弦定理の出題頻度が増えています。なぜ、増えているのか？そして、それはよいことです。どのように良いことなのか？
それを書こうと思いましたが、まず第1余弦定理がどのようなものかわからなければ、話が進みませんので、仕方ないのでここで紹介します。
第1余弦定理とは
公式の形で言うと a=bcosC+ccosBです。
こんな公式どうでもいいです。忘れてください。
ここで確認したいのは、第1余弦定理という考え方です。
次のような問題で使います
①図
ＡＢ＝２、ＡＣ＝√2、∠Ｂ＝３０゜、∠Ｃ＝４５゜のとき、ＢＣの長さを求めなさい。
こういう問題です。
∠Ａの大きさは１８０゜―（３０゜＋４５゜）＝１０５゜です。cos105゜がよくわからないので、いわゆる余弦定理は使えません。
ここで使うのが、中学の最後で習った特別な直角三角形の辺の比です
３０゜‐６０゜‐９０゜の直角三角形の辺の比は１：２：√３、
４５゜‐４５゜‐９０゜の直角三角形の辺の比は１：１：√２でした。
これを使って答えを導きます。
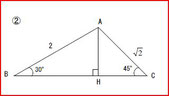
②まず、頂点Ａから辺ＢＣに垂線ＡＨを引きます。
③△ＡＢＨは、３０゜‐６０゜‐９０゜の直角三角形です。
ＡＢ＝２より、ＢＨ＝√３とわかります。
④△ＡＣＨは、４５゜‐４５゜‐９０゜の直角二等辺三角形です。
ＡＣ＝√２より、ＣＨ＝１とわかります。
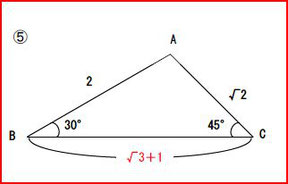
⑤したがってＢＣ＝√３＋１となります。
数値としては一番簡単なものを扱いましたが、出される角度は決まっているので、辺の長さがこれら以外の値でも簡単な比の計算で求めることができます。
これが第１余弦定理です
要約すると一番最初にあげた公式のようになりますが、この特別な直角三角形の比を使いこなすこの考え方そのものが第１余弦定理と考えてよいです。
今、このタイプの問題の出題頻度が増えています。それはとても良いことです。
それについては、別の機会に詳しく書かせて頂こうと考えています。
シェア歓迎します。リンクもフリーです。