正弦波の式の作り方
高校物理で「波」は苦手とする人が多い単元です。
特に、正弦波の式・・・

・・・なかなかすぐには、なじめませんよね。
「こんなのどうやって覚えればいいんだ」…と思っている人も多いかもしれません。
が・・・
覚える必要は、ありません。
・・・こういうと誤解があるかもしれませんね。
厳しい言い方をすると・・・
「これを覚えて、あてはめれば済むような問題は、ほとんどない」…ということです。
自分でこの式を導いて、その「意味」が理解できていないと、物理のテストでの得点力はほとんど望めないということです。(みなさん、それは実感がありますよね。)
市販の物理の問題集でも、この式を導くタイプの問題や、導く際に使った考え方を活かす問題は必ず掲載されています。物理では問題を通して理解を深めていくのが有効なので、そういう問題をていねいにこなしていけばいいです。
でも、それが難しいという人がけっこういるのも、無理のないことともいえます。
そこで、今回の解説記事では・・・
正弦波の式の導き方(導出法)
・・・について、みていきます。
本来、「等速円運動」からみていくべきなのですが、焦点をしぼるためここでは簡単な確認にとどめ、「正弦波の式」に集中します。
「等速円運動」→「単振動」→「波の発生」
要点だけ確認していきます。

左図のように等速円運動をしている物体があるとします。
それを、あなたは真横からみているとしましょう。
(本当に真横です。パソコンやスマホの真横からみることをイメージしましょう。)
みなさんからみて、その物体は・・・
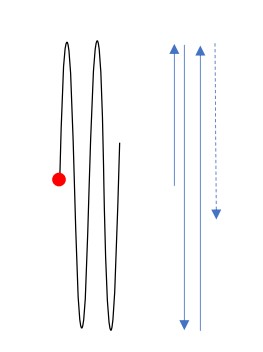
単振動・・・しているようにみえますよね。
(私は昔、天ぷら屋で働いていたこともあるのですが、そこでは、まな板より少し大きいくらいの大根おろし器で円運動でするのですが、そのときこれ〔単振動=等速円運動を真横からみたもの〕を実感しました。)
一方、波は媒質の1点が単振動することによって生じます(周りに広がっていきます)。
単振動は、円(等速円運動)がもとなので、あたりまえに変位や速度などの要素を三角比を使って表せました。
よって、単振動を元とする波の式も、三角比を用いて表されます。
それが、「正弦波の式」です。
正弦波の発生
ここで、「正弦波の発生(媒質の1点が単振動)」からみていくのが普通ですが、・・・やめておきましょう。
ここでは、すでに発生し進行している波を元に考えてみます。実際、その方が考えやすいです。
下図の波は、赤矢印の方向に進んでいて、図はある時間における波の変位のようすであるとします。
新体操のリボンを真横からみていると考えていいですよ。

波のグラフで気をつけないといけないことは、それが・・・
y - t グラフ(ある位置での、時間〔 t 〕と変位〔 y 〕の関係を表したグラフ)か、
y - x グラフ(ある時間での、位置〔 x 〕と変位〔 y 〕の関係を表したグラフ)かを、
しっかり意識して区別することです。
上図は、新体操のリボンを横からみたもの…としましたので、「y - x グラフ」にあたります。
平面(2次元)の関係(関数)だけでなく、それにもう1本、軸が加わることになります。
難しいのは無理はないですよね。(とはいえ、そんなに高度なことが求められているというわけではなく、必要に応じて、平面を切り出して、それを積み重ねていけば大丈夫です。)
では、上図を元にした「y - t グラフ」を考えてみましょう。
大切なのは、自分で自主的に「基準」を決めることです。
波を横からみて上図の形になっている時間を、「t=0」としましょう。
「x=0」をどこにするか、上図をみてみなさんも少し考えてみましょう。
正弦波の式の導き方のコツ
「コツ」です。
一般の教科書・参考書など、すべてこうしていますが、
こうしなければいけないというものではなく、こうするとわかりやすい…ということです。
この形で、y =sin x の形になるところをx =0としてもいいのですが、
x=0の位置における時間 t による変化が、わかりやすいところにしましょう。
図の波は右向きに進行しています。
この図の時点で変位が0で、これから大きくなっていくところを選びましょう。

この位置でいいですね。ここを、x=0としましょう。
波がこの図の形になった時刻を t=0とし、x=0の位置における「y - t グラフ」は次図のようになります。

図のように振幅をA〔m〕、周期をT〔s〕とします。
この形なので、「y=Asin〇」というsinを使った式で表されます。
(そうなるように x=0の位置を決めました。)
周期というのは1回振動するのにかかる時間(〔秒〕単位)で、ここでは変位が0の位置から上がって下がってまた上がって再び0になるまでの時間と考えるといいでしょう。
波を表す式の角度を表す部分を位相といいます。
「y=Asin〇」の「○」の部分のことです。
三角比なので、0から2π(円運動で1回転)で、1周期です。
この位相の部分を、簡単に起こせる(表せる)ようになることが今回の解説記事の目的です。
単振動からでなく、この形から解釈できるようにする…と言ってもいいでしょう。
ここで、『算数』で勉強したことを使います。
正弦波の位相の求め方 その1

位相が、0から2πまで「2π」変化するのにかかる時間が、周期の T〔秒〕です。
1〔秒〕あたりの位相の変化は、わり算で 2π ÷ T より・・・

・・・と、表されます。
(単位の、[rad]は〔ラジアン〕、[s]は〔秒〕のことです。)
(なお、この「2π/ T」は、等速円運動でいうところの角速度 ω〔rad/s〕にあたります。)

t 秒後の位相は、1秒あたりの位相の変化量である「2π/T」に、それが何秒分かにあたる t をかければよく、「(2π/T)×t」より・・・

・・・と、表されます。
なお、こういうのが好きな人がけっこういますので、単位の部分の計算(かけ算)
をみてみますと・・・

〔rad / s〕単位の数値に〔s〕(秒)をかけることによって、分母の〔s〕が払われ、〔rad〕単位(ラジアン単位)の数値に変換されていることが分かります。
以上より、x=0 の位置でのt秒後の位相(「sin〇」の「○」の部分)が決まり、
x=0 の位置の変位 y は、次の式で表されるとわかります。
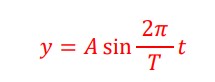
次に、この式を元に一般に x の位置・・・x=0 以外の位置も含め、y を t と x で表した式・・・を考えていきます。
・・・と思いましたが、その前にもう1つ、この位相「(2π/T)×t」の導き方を確認しておきます。
これも、算数の学習内容を使います。
正弦波の位相の求め方 その2

「2π」で1周期なので、これを(全体)と考えます。
T秒で1周期なのですが、t 秒後にはそのうちの t 秒分だけ進んでいます。
その(割合)は分数で・・・

・・・と、表されます。
よって、t秒後の位相は(全体)にこの(割合)をかけ・・・

・・・と表されるとわかります。(少し形が違うだけで、先ほどの「(2π/T)×t」と同じものだということは、いいですよね。)
正弦波の式の一般式
それでは、位置xでのt秒後の変位yについてみていきましょう。
波の進む速さを v〔m/s〕とします。
イメージしやすいように、下図のようにx=0から波長の半分分進んだ位置の変位を考えてみましょう。
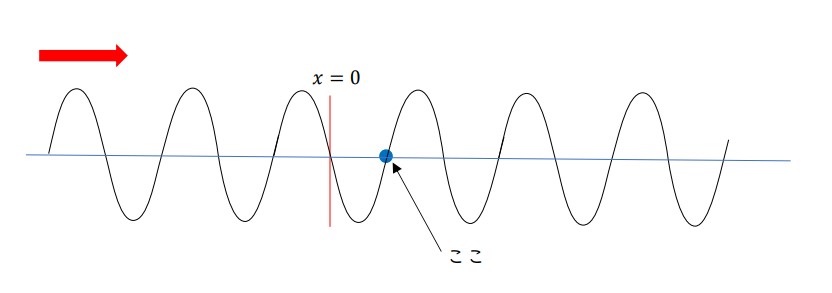
この位置では、波が半分分進むとx=0 と同じ変位になり、それからx=0 と同じような変位の変化をすることになります。
位置xでは、位置x=0 における波が伝わってきてから、同じように振動を始める・・・と考えればいいですね。
位置xに位置x=0 における波が伝わるまでにかかる時間は、距離xを速度vで進むときにかかる時間なので、わり算で

・・・と表されます。
位置xにおいては、x/v秒後にx=0 と同じ振動が始まります。
上で求めたx=0 における変位の式で、tを・・・

・・・とすることで、位置xにおける変位の式が求められます。

これで、目標の正弦波の式が完成です。
後はこれを、目的に応じて変形します。
まず変位の部分の(1/T)をかっこの中に入れて・・・

ここで、


これで、トップ画像の式が求められました。
(v=λ /T についての解釈は焦点がぼやけるのでここではやめておきます。各自考えてみましょう。)
なお、・・・
波の基本公式 v= f λ
・・・は、基本公式と言われるだけあって、汎用性が高いです。使いこなせるようにしておきましょう。
v = λ/ T も、ここから導けます。
(別の場所でこれにも触れようと思いますが、とりあえず『算さば』のトップページに考え方のまとめがありますので、そちらもどうぞ。)
私が『算数』の大切さ(かけ算・わり算の意味の大切さ)に目覚めたのも「v=fλ」がきっかけでした。
正弦波の式を y - x グラフから。
y -x グラフからも、正弦波の式を求めることができます。
最初に扱った図で、x=0 と決めたところをかきだすと、次のような形になります。

この場合、y=0から、下がって上がってまたさがるので、
「y=-Asin○」・・・という形の式になります。
後は、各自考えてみましょう。
とりあえず「てびき」だけ示しておきますと・・・
①「位相」の部分は、(全体)×(割合)の考え方が、わかりやすいでしょう。
②t秒後、波はvt進むので、「x」を「x-vt」とします。
ここが、わかりにくいかもしれませんが、数学で勉強した「軌跡」の考えを使ってみましょう。
(ここのわかりやすい考え方も、いずれ紹介するつもりです。)
③「sin(-θ)=-sinθ」の公式で、タイトル画の式の形にピッタリ近づけられます。
④波の基本公式「v=fλ」を使って、自在に変形しましょう。
以上です。
ご意見・ご感想お待ちしております。
執筆:井出進学塾 井出真歩
コメントもお待ちしています。


富士宮教材開発 (水曜日, 05 6月 2024 17:58)
to たん様
とりあえず、形式的な解説になりますが・・・
t 秒後、グラフは右に vt だけ進んでいます。
もとのグラフ上の点(x、y)が t 秒後に移った点を(X、Y)とすると、
X=x+vt 、Y=y であり、これより x=X-vt、y=Y
これらを、元の式の x、y に代入し、
X→x、Y→yとすれば、上式が導かれます。
数学の「グラフの平行移動」のところを、見直しておくとよいかと思います。
たん (月曜日, 03 6月 2024 21:33)
一番最後はどうしてvtを引いてるんですか?